●互补滤波
互补滤波器，也是带通滤波器的变种。
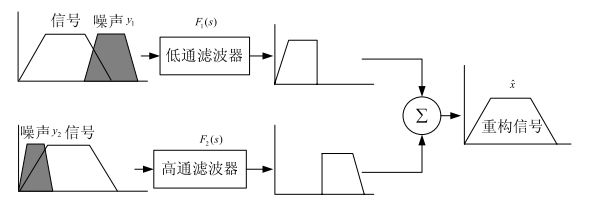
低通滤波器（英语：Low-pass filter）容许低频信号通过，但减弱（或减少）频率高于截止频率的信号的通过。’低’和’高’频率的含义，是相对于滤波器设计者所选择的截止频率而言的。 高通滤波器则相反，而带通滤波器则是高通滤波器和低通滤波器的组合。
互补滤波原理
假如我们对一个物理量有两种测量手段，一种容易受到高频噪声的干扰，实际的观感就是信号有很多的毛刺；另一种容易受到低频噪声的干扰，就是噪声会慢慢的变化。那么我们就可以设计互补的两个滤波器 F1和F2，所谓互补就是 F1+F2=1 ，它们一个是低通滤波器，可以滤除信号中的高频噪声，一个是高通滤波器，能够滤除信号中的低频变化。这样分别把相应测量中的噪声滤除，就可以得到更精确的对这个物理量的测量了。
\(\begin{align}
低通滤波器：F_{lp}(s) &= \cfrac{C(s)}{C(s)+s}\\
高通滤波器：F_{hp}(s) &= 1 -F_{lp}(s)
= \cfrac{s}{C(s)+s}
\end{align}\)
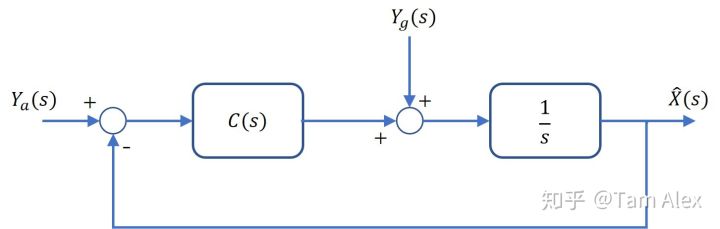
从频域角度看，我们完全可以把测得的加速度Ya(s)认为是测得姿态，因为中间只是经过代数运算而没有积分或微分（意思是通过代数运算获得的姿态实际上频率特性和Ya(s) 是一致的)。而陀螺测得的角速度则需要积分才能得到姿态，因此我们认为 Yg(s)/s 表示测得的姿态（实际上就是角度）。
\[下面把F_{lp}(s)施加给y_a，把F_{hp}(s)施加给y_g/s，得到 \\ \begin{align} \hat X(s) &= \cfrac{C(s)}{C(s)+s}Y_a(s) + \cfrac{s}{C(s)+s}\cfrac{Y_g(s)}{s}\\ &= \cfrac{C(s)Y_a(s)+Y_g(s)}{C(s)+s} \end{align}\]实际上可以表示为下面控制框图
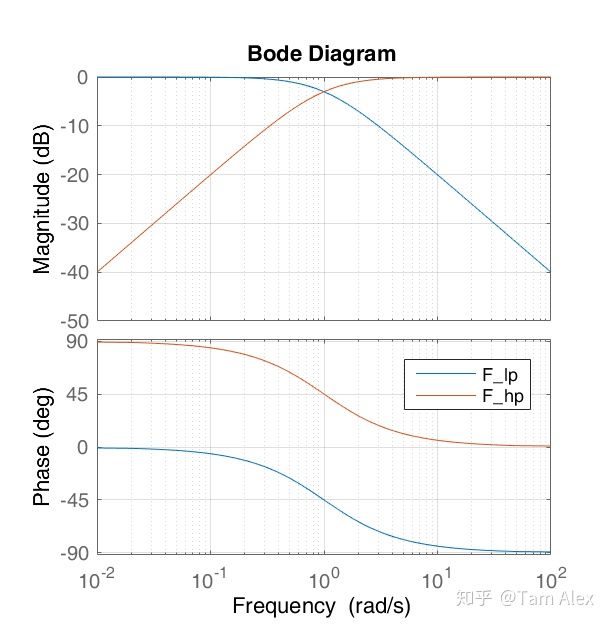
令C(s)=1，则高低通滤波器的波特图为：
\(随着 C(s)取不同的形式，两个滤波器的阶次也会随之变化，比如：\\
当C(s)= \alpha时，滤波器阶数为一阶。
\\F_{lp}(s) = \cfrac{\alpha}{\alpha+s}, 即时间常数为\cfrac{1}{\alpha}的一阶低通滤波器，\\F_{hp}(s) = 1 -F_{lp}(s)= \cfrac{s}{\alpha+s}\\
当C(s)= \alpha + \cfrac{\beta}{s}时，滤波器阶数为二阶。
\\F_{lp}(s) = \cfrac{\alpha + \cfrac{\beta}{s}}{\alpha + \cfrac{\beta}{s}+s}=\cfrac{\alpha s+\beta}{s^2+\alpha s+\beta}, \\F_{hp}(s) = 1 -F_{lp}(s)= \cfrac{s^2}{s^2+\alpha s+\beta}\)
基本互补滤波
陀螺仪可以通过积分获得一组姿态，而加速度计(配合磁强计)也能够获得一组姿态，但是加速度计的特性是对震动非常灵敏（高频噪声），因此短时间内可信度低。陀螺仪容易受到漂移（低频噪声），积分的姿态角会一直跑偏，因此长时间内可信度低。我们按照上面原理，直接设计姿态互补滤波器。
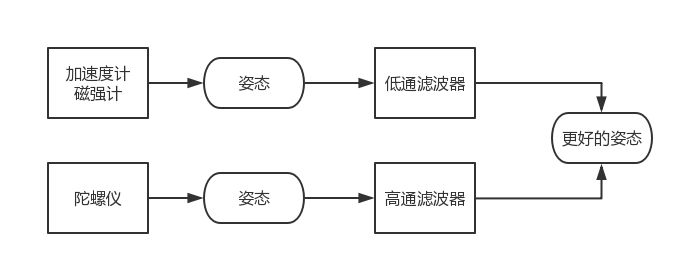
实际中采用的姿态互补滤波器（PI控制）
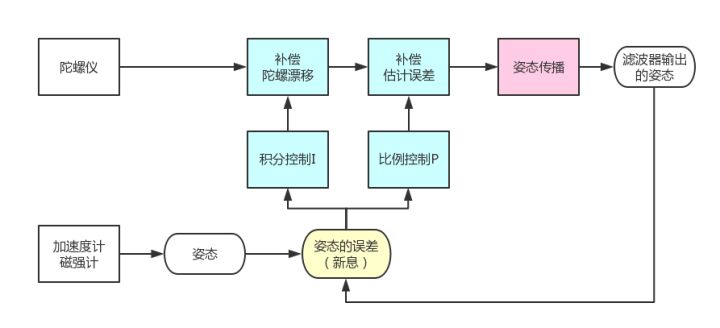
一阶互补滤波
float ComplementaryFilter1(float acc_m, float gyro_m)
{
float K = 0.02; // 对加速度计取值的权重
float angle = K * acc_m + (1-K) * (angle + gyro_m * dt);
return angle;
}
其中，angle为得到的实际角度，gyro_m为陀螺仪值，acc_m为加速度数据换算后的角度值，dt为滤波器采样时间；即通过调整一个加权系数K，如果陀螺仪所占的权重大些，则解算的角度则跟陀螺角度近似，加速度类似。
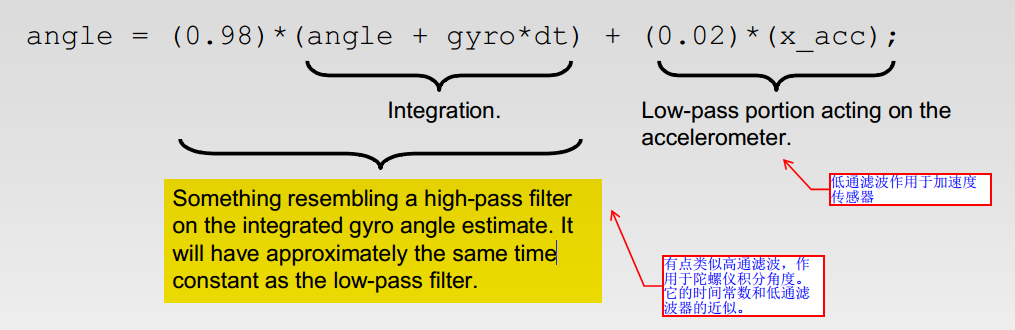
二阶互补滤波
float ComplementaryFilter2(float acc_m, float gyro_m)
{
float k = 0.05;// 对加速度计取值的权重
float x1 = (acc_m - angle) * k * k;
float y1 = y1 + x1 * dt;
float x2 = y1 + 2 * k * (acc_m - angle) + gyro_m;
float angle = angle + x2 * dt ;
return angle;
}
Mahony的互补滤波器
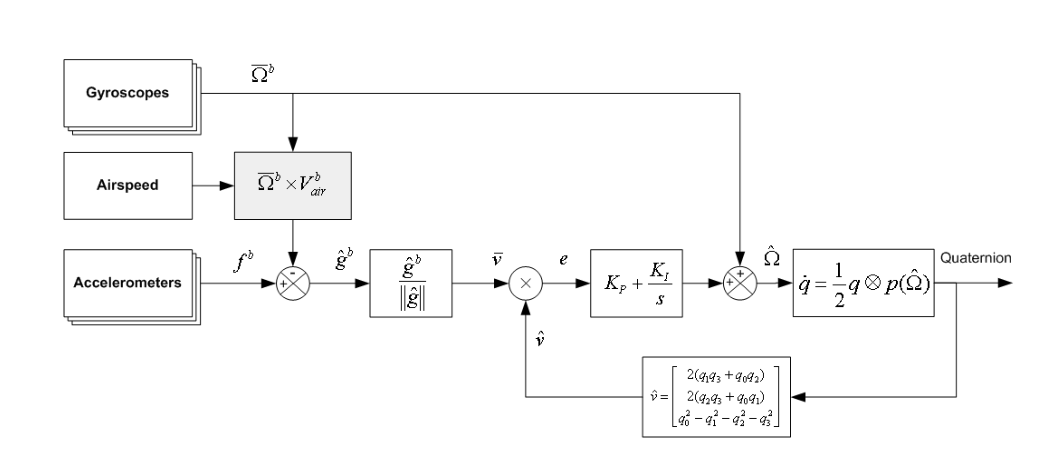\(从图中可以看出，加速度传感器测的数据f^b并没有直接被g^b拿来使用。而是通过\bar\Omega^b×V_{air}^b进行了修正。
\\它的目的就是消除飞行过程中的运行加速度，从而更好的还原重力加速度。\)
传统互补滤波器我们可能使用欧拉角相减，DCM或四元数相乘来获取姿态的误差，这样的方法都有一个缺点，那就是需要通过加速度计和磁强计的测量计算出一组姿态。虽然常用的方法比较成熟，但也有一些问题，比如欧拉角法存在奇异点（如在俯仰角90度时），DCM和四元数的TRIAD或QUEST等方法又需要额外的计算Mahony的突出贡献之一就是直接利用加速度计和磁强计的测量值，利用和惯性空间向量的叉乘，简简单单的就获得了姿态的误差。
Mahony的另一个突出贡献就是证明了这类互补滤波器的稳定性。上面我们讲了，互补滤波器不存在某种准则下的最优，但对于滤波器是否能够收敛以往的证明也是不很完善的。Mahony在那篇论文里不但证明了这一类互补滤波器的几乎全局渐近稳定，还证明了其不稳定集是一个不变集，给实际使用提供了非常完备的理论支持。
●卡尔曼滤波
卡尔曼滤波器适用于线性系统，设该系统的状态方程和观测方程为： \(\left\{\begin{array}{1} x_k=Ax_{k-1}+Bu_k+w_k\\ z_k=Hx_k+v_k\\ \end{array}\right.\)
\[\begin{align} x_k&--k时刻系统的状态 \\ u_k&--k时刻对系统的控制量 \\ w_k&--过程噪声，其协方差为Q\\ z_k&--k时刻的测量值\\ v_k&--测量噪声，其协方差为R \\ A、B、H&--系统参数，多输入多输出时为矩阵，单输入单输出时为常数 \end{align}\]卡尔曼滤波原理
卡尔曼滤波（Kalman filtering）一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。
基本思想是根据当前的状态，预测下一时刻的状态，结合测量，得到最优状态。可以用于预测、跟踪。
卡尔曼有五个黄金公式，前两个是预测公式，后三个是更新公式，卡尔曼就是通过计算预测值和测量值的方差之比来估计预测值和测量值占真值的权重，即更相信哪个值。 \(\begin{align} x_k&--状态的真实值 \\ \tilde x_{\bar{k}}&--状态的预测值，也称先验状态估计值 \\ \tilde x_k&--状态的最优估计值，也称后验状态估计值 \\ P_\bar k&--先验估计误差的协方差 \\ P_k&--后验估计误差的协方差 \\ \end{align}\)
\[预测方程 \begin{align} \tilde x_{\bar{k}}&=A\tilde x_{k-1}+Bu_k \tag{1} &&向前推算状态变量\\ P_{\bar{k}}&=AP_{k-1}A^T+Q \tag{2} &&向前推算误差协方差 \\ \end{align}\] \[更新方程 \begin{align} K&=\cfrac{P_{\bar k}H^T}{HP_{\bar k}H^T+R} \tag{3} &&计算卡尔曼增益\\ \tilde x_k&=\tilde x_{\bar k}+K(z_k-H\tilde x_{\bar k}) \tag{4} &&由观测变量z_k更新估计\\ P_k&=(I-KH)P_\bar k \tag{5} &&更新误差协方差\\ \end{align}\]原理实现
下面用通俗的说法说明一阶卡尔曼公式。
用K-1时刻的值来预测当前k时刻的状态值X(K|K-1)和误差协方差P(K|K-1)。
(K|K-1)表示用K-1时刻的值来算K时刻，表示是预测的。
(K-1|K-1)表示K-1时刻的最优值。(K|K)表示K时刻的最优值，是最终需要得到的值。
条件：控制量u(k)=0;参数A和H也简单地取1
预测公式：
X(K|K-1) = X(K-1|K-1) //假设每一时刻的值是不变化的。
P(K|K-1) = P(K-1|K-1)+Q //Q是过程噪声，代表测得预测值的准确与否。
更新公式：
Kg =P(K|K-1)/(P(K|K-1)+R) // R是测量噪声，代表测量噪声，即采集数据的波动
// Kg是卡尔曼增益。R越小，Kg越大，表示越相信测量值，Kg代表相信测量值的程度
X(K|K) = (1 – Kg)·X(K|K-1) + Kg·Z(K) //相信预测值1-Kg，相信测量值Kg。算出此刻的最优值
P(K|K) = (1 – Kg)·P(K|K-1) //更新此刻的协方差。相信原来值的1-Kg。
/********************************************************************
* Function Name : kalmanFilter
* Description : 卡尔曼滤波
* Input : KFP input
* Output : None
* Return : out
Q:过程噪声，Q增大，动态响应变快，收敛稳定性变坏，系统噪声
R:测量噪声，R增大，动态响应变慢，收敛稳定性变好
input: ADC采集的数据
注：1 A=1； 控制量：U(k)=0;
2 个人感觉float足够用了，double太浪费了！
如果用户感觉精度不够，可以改为double
*******************************************************************************/
//1. 结构体类型定义
typedef struct
{
float LastP;//上次估算协方差 初始化值为0.02
float Now_P;//当前估算协方差 初始化值为0
float out;//卡尔曼滤波器输出 初始化值为0
float Kg;//卡尔曼增益 初始化值为0
float Q;//过程噪声协方差 初始化值为0.001
float R;//观测噪声协方差 初始化值为0.543
}KFP；//Kalman Filter parameter
//2. 以高度为例 定义卡尔曼结构体并初始化参数
KFP KFP_height={0.02,0,0,0,0.001,0.543};
/**
*卡尔曼滤波器
*@param KFP *kfp 卡尔曼结构体参数
* float input 需要滤波的参数的测量值（即传感器的采集值）
*@return 滤波后的参数（最优值）
*/
float kalmanFilter(KFP *kfp,float input)
{
//预测协方差方程：k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
kfp->Now_P = kfp->LastP + kfp->Q;
//卡尔曼增益方程：卡尔曼增益 = k时刻系统估算协方差 / （k时刻系统估算协方差 + 观测噪声协方差）
kfp->Kg = kfp->Now_P / (kfp->NOw_P + kfp->R);
//更新最优值方程：k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * （测量值 - 状态变量的预测值）
kfp->out = kfp->out + kfp->Kg * (input -kfp->out);//因为这一次的预测值就是上一次的输出值
//更新协方差方程: 本次的系统协方差付给 kfp->LastP 威下一次运算准备。
kfp->LastP = (1-kfp->Kg) * kfp->Now_P;
return kfp->out；
}
/**
*调用卡尔曼滤波器 实践
*/
float height,kalman_height;
kalman_height = kalmanFilter(&KFP_height,(float)height);
参考文献：
C语言实现：
