●姿态解算介绍
姿态解算需要解决的是无人机飞行器在地球坐标系中姿态。
姿态解算的英文是attitude algorithm,也叫做姿态分析,姿态估计,姿态融合。姿态解算是指把IMU(陀螺仪、加速度计)、罗盘等的数据融合在一起,得出飞行器的空中姿态。
IMU:惯性测量单元(Inertial Measurement Unit),包含陀螺仪,加速度计。IMU将所有运动视作直线运动与旋转运
动的总和,因而通过加速度计测得直线运动,通过陀螺仪测得旋转运动,进而和初始姿态相对比,得到当前的状态与相对位移,
并不依赖外部的重力场或磁场,可以在任何情况下使用(精度够高的话)。
AHRS: Attitude and Heading Reference System 中文译称“航姿参考系统”,包含陀螺仪,加速度计,电子罗盘。通过地球的重力场,磁场来判读自身的姿态与位置,磁场重力场越正交,精度效果越好,因而在高纬度地区误差大。
飞行器根据陀螺仪的三轴角速度对时间积分得到的俯仰/横滚/航向角,这是快速解算。快速解算得到的姿态是存在误差的,而且误差会累加,如果再结合三轴地磁和三轴加速度数据进行校正,得到准确的姿态,这就是深度解算。
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量,欧拉角最直观,轴角表示则适合几何推导,而在组合旋转方面,四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存飞行器的姿态。
姿态控制算法的输入参数必须要是欧拉角。
●四元数姿态解算流程
Mahony算法
IMU融合算法
1、初始化四元数
\(q = \begin{bmatrix}
q_0 \\
q_1 \\
q_2 \\
q_3
\end{bmatrix}
= \begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}\)
2、获取角速度、加速度
读取三轴陀螺仪的测量值即角速度w.x、w.y、w.z,三轴加速度计的测量值即加速度acc.x、acc.y、acc.z。
3、重力加速度归一化
将三轴加速度计的测量值acc.x、acc.y、acc.z,转化为三维的单位向量(规范化)。得到:
\(\left\{\begin{array}{1}
a.x=\cfrac{acc.x}{\sqrt{acc.x^2+acc.y^2+acc.z^2}}\\
a.y=\cfrac{acc.y}{\sqrt{acc.x^2+acc.y^2+acc.z^2}}\\
a.z=\cfrac{acc.z}{\sqrt{acc.x^2+acc.y^2+acc.z^2}}\\
\end{array}\right.\)
4、提取四元数等效余弦矩阵中的重力分量v.x、v.y 、v.z
四元数与旋转矩阵:
\(\begin{align}
R_b^e &= \begin{bmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2)\\
2(q_1q_2+q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1)\\
2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & q_0^2-q_1^2-q_2^2+q_3^2
\end{bmatrix}\\
&= \begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}\\
\end{align}\)
重力矩阵[0 0 1]左乘上面矩阵 即可提取出重力分量,即第三列
\(\left\{\begin{array}{1}
v.x= 2(q_1q_3+q_0q_2)\\
v.y= 2(q_2q_3-q_0q_1)\\
v.z= 1-2(q_1^2+q_2^2)
\end{array}\right.\)
5、求取加速度计测出来的重力向量和陀螺积分后的重力向量之间的误差(它们都是机体坐标参照系上的重力向量) ,作为陀螺仪修正量:
\(\vec{a}\times\vec{b} = |a| |b| \sin{\theta}\)
向量的叉积可以用来判断两个向量是否平行,当两个向量都为单位向量的时候,它们之间的叉积就代表了它们之间的平行度,若平行则叉积为0,若垂直则叉积为1,两向量的方向差越小,叉积也越小,因此可以用叉积来表示两归一化向量的方向误差
向量间的误差,可以用向量叉积(也叫向量外积、叉乘)来表示。
\(\begin{bmatrix} ex \\ey \\ez \end{bmatrix}=
\begin{bmatrix} a.x \\a.y\\a.z\end{bmatrix} \times
\begin{bmatrix} v.x \\v.y\\v.z\end{bmatrix} =
\begin{bmatrix} a.y*v.z-a.z*v.y \\a.z*v.x-a.x*v.z \\a.x*v.y-a.y*v.x \end{bmatrix}\)

这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。
6、利用得到的误差对陀螺仪的测量值进行修正(实际上进行了一次PI控制):
其中,Kp和Ki是一个调整参数,需在实际调试中来确定。其中,Ki可以等于0,Kp可以以0初始,0.01为为步进调节。Kp可看作加速度权重,越大则向加速度测量值收敛越快。
实际上这种修正方法只把b系和n系的XOY平面重合起来,对于z轴旋转的偏航,由于加速度计无法感知z轴上的旋转运动,所以还需要用地磁计来进一步补偿。
7、利用修正后的陀螺仪数值,更新四元数:
一阶毕卡近似算法:
\(\left\{\begin{array}{1}
q_0= q_0 + \cfrac{T}{2}(-q_1w_{xint}-q_2w_{yint}-q_3w_{zint}) \\
q_1= q_1 + \cfrac{T}{2}(q_0w_{xint}+q_2w_{zint}-q_3w_{yint}) \\
q_2= q_2 + \cfrac{T}{2}(q_0w_{yint}-q_1w_{zint}+ q_3w_{xint}) \\
q_3= q_3 + \cfrac{T}{2}(q_0w_{zint}+q_1w_{yint}-q_2w_{xint}) \\
\end{array}\right.\)
8、将得到更新后的四元数规范化
\(\left\{\begin{array}{1}
q_0=\cfrac{q_0}{\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}}\\
q_1=\cfrac{q_1}{\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}}\\
q_2=\cfrac{q_2}{\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}} \\
q_3=\cfrac{q_3}{\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}}
\end{array}\right.\)
规范化四元数作用:
(1).表征旋转的四元数应该是规范化的四元数。但是由于计算误差等因素,使得计算的变换四元数的模不再等于1,计算过程中四元数会逐渐失去规范化特性,因此必须对四元数做规范化处理
(2).单位化四元数在空间旋转时是不会拉伸的,仅有旋转角度.这类似与线性代数里面的正交变换。单位化的四元数可以表示一个旋转。
9、将此四元数递归回到开头,将旧的四元数更新为新四元数,作为下一次四元数运算的的初始四元数,再从1开始下一次的四元数运算。
同时,根据四元数方向余弦阵和欧拉角的转换关系,把四元数转换成欧拉角 pitch(Θ)、 roll(Φ)、yaw(Ψ),完成了姿态的初步运算。
四元数与欧拉角:
\(\left\{\begin{array}{1}
\theta= -\arcsin{r_{31}}\\
\phi= \arctan{\cfrac{r_{32}}{r_{33}}} \\
\psi= \arctan{\cfrac{r_{21}}{r_{11}}}
\end{array}\right.\)
例程如下:
void imuUpdate(Axis3f acc, Axis3f gyro, state_t *state , float dt) //数据融合、互补滤波
{
float normalise;
float ex, ey, ez;
float halfT = 0.5f * dt;
float accBuf[3] = {0.f};
Axis3f tempacc = acc;
gyro.x = gyro.x * DEG2RAD; //度转弧度
gyro.y = gyro.y * DEG2RAD;
gyro.z = gyro.z * DEG2RAD;
//加速度计输出有效时,利用加速度计补偿陀螺仪
if((acc.x != 0.0f) || (acc.y != 0.0f) || (acc.z != 0.0f))
{
//单位化加速度测量值
normalise = invSqrt(acc.x * acc.x + acc.y * acc.y + acc.z * acc.z);
acc.x *= normalise;
acc.y *= normalise;
acc.z *= normalise;
//加速计读取的方向与重力加速计方向的差值,用向量又乘计算
ex = (acc.y * rMat[2][2] - acc.z * rMat[2][1]);
ey = (acc.z * rMat[2][0] - acc.x * rMat[2][2]);
ez = (acc.x * rMat[2][1] - acc.y * rMat[2][0]);
//误差累计,与积分常数相乘
exInt += Ki * ex * dt ;
eyInt += Ki * ey * dt ;
ezInt += Ki * ez * dt ;
//用叉积误差来做PI修正陀螺零偏,即抵消陀螺读数中的偏移量
gyro.x += Kp * ex + exInt;
gyro.y += Kp * ey + eyInt;
gyro.z += Kp * ez + ezInt;
}
//一阶近似算法,四元数运动学方程的离散化形式和积分
float q0Last = q0;
float q1Last = q1;
float q2Last = q2;
float q3Last = q3;
q0 += (-q1Last * gyro.x - q2Last * gyro.y - q3Last * gyro.z) * halfT;
q1 += ( q0Last * gyro.x + q2Last * gyro.z - q3Last * gyro.y) * halfT;
q2 += ( q0Last * gyro.y - q1Last * gyro.z + q3Last * gyro.x) * halfT;
q3 += ( q0Last * gyro.z + q1Last * gyro.y - q2Last * gyro.x) * halfT;
//单位化四元数
normalise = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= normalise;
q1 *= normalise;
q2 *= normalise;
q3 *= normalise;
imuComputeRotationMatrix(); //计算旋转矩阵
//计算pitch roll yaw 欧拉角
state->attitude.pitch = -asinf(rMat[2][0]) * RAD2DEG;
state->attitude.roll = atan2f(rMat[2][1], rMat[2][2]) * RAD2DEG;
state->attitude.yaw = atan2f(rMat[1][0], rMat[0][0]) * RAD2DEG;
}
void imuComputeRotationMatrix(void)
{
rMat[0][0] = 1.0f - 2.0f * q2q2 - 2.0f * q3q3;
rMat[0][1] = 2.0f * (q1q2 -q0q3);
rMat[0][2] = 2.0f * (q1q3 +q0q2);
rMat[1][0] = 2.0f * (q1q2 +q0q3);
rMat[1][1] = 1.0f - 2.0f * q1q1 - 2.0f * q3q3;
rMat[1][2] = 2.0f * (q2q3 -q0q1);
rMat[2][0] = 2.0f * (q1q3 -q0q2);
rMat[2][1] = 2.0f * (q2q3 +q0q1);
rMat[2][2] = 1.0f - 2.0f * q1q1 - 2.0f * q2q2;
}
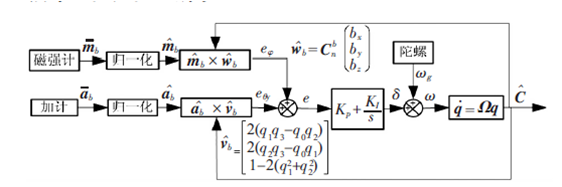
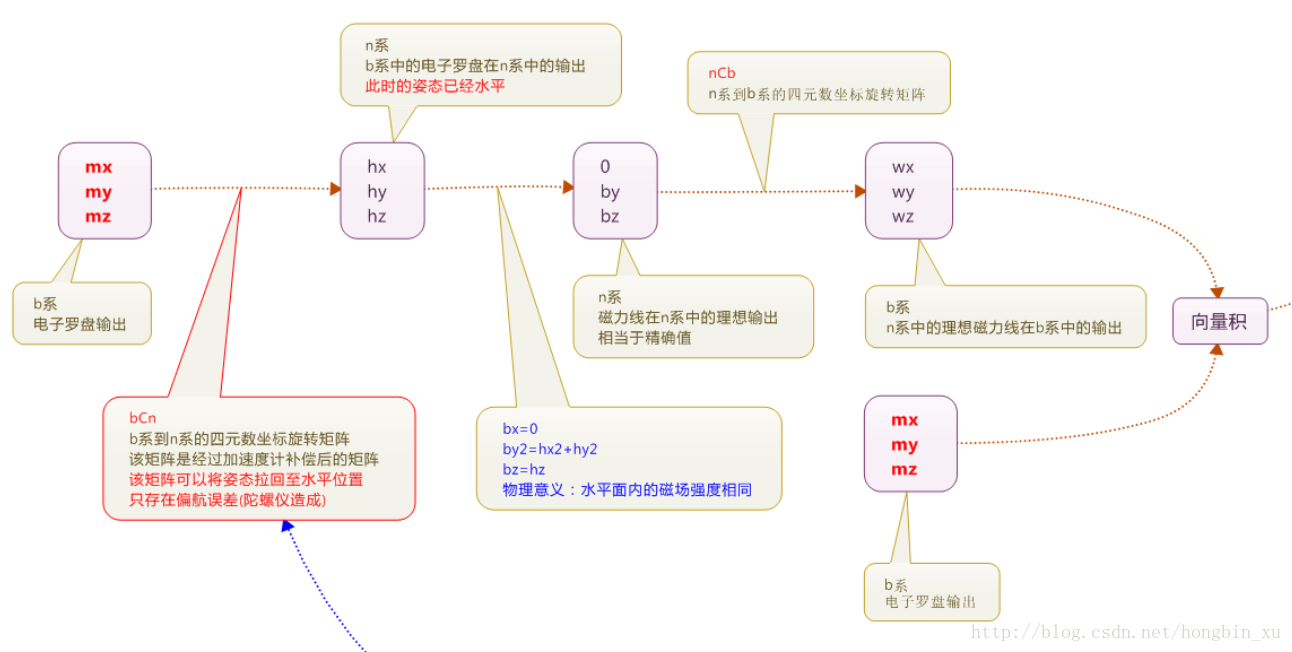
AHRS融合算法
1、三轴地磁数据归一化 \(\left\{\begin{array}{1} m.x=\cfrac{m.x}{\sqrt{m.x^2+m.y^2+m.z^2}}\\ m.y=\cfrac{m.y}{\sqrt{m.x^2+m.y^2+m.z^2}}\\ m.z=\cfrac{m.z}{\sqrt{m.x^2+m.y^2+m.z^2}} \end{array}\right.\)
2、计算参考方向
用归一化的数据右乘四元数旋转矩阵得到参考方向 ,即将这组机体坐标系b下测得的数据旋转到导航坐标系e下,得到:
\(\begin{bmatrix}
h.x \\
h.y \\
h.z
\end{bmatrix} =
\begin{bmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2)\\
2(q_1q_2+q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1)\\
2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & q_0^2-q_1^2-q_2^2+q_3^2
\end{bmatrix}
\begin{bmatrix}
m.x \\
m.y \\
m.z
\end{bmatrix}\)
让地磁X轴对准北方,则地磁在此坐标系下应为[b.x 0 b.z],参考方向要与此坐标系下方向一致,则有
\(\left\{\begin{array}{1}
b.x^2 = h.x^2 + h.y^2 \\
b.z = h.z
\end{array}\right.\)
现在我们假设R旋转矩阵是经过加速度计校正后的矩阵,当某个确定的向量(b系中)经过这个矩阵旋转之后(到e系),这两个坐标系在XOY平面上重合,只是在z轴旋转上会存在一个偏航角的误差。下图表示的是经过R旋转之后的b系和e系的相对关系。可以明显发现加速度计可以把b系通过四元数法从任意角度拉到与e系水平的位置上,这时,只剩下一个偏航角误差。
在这个XOY平面上(e系),的投影为(b.x)2,的投影为(h.x)2+(h.y)2。显然,地磁计在XOY平面上(e系)的向量的大小必定相同,所以有b.x2= h.x2+h.y2。
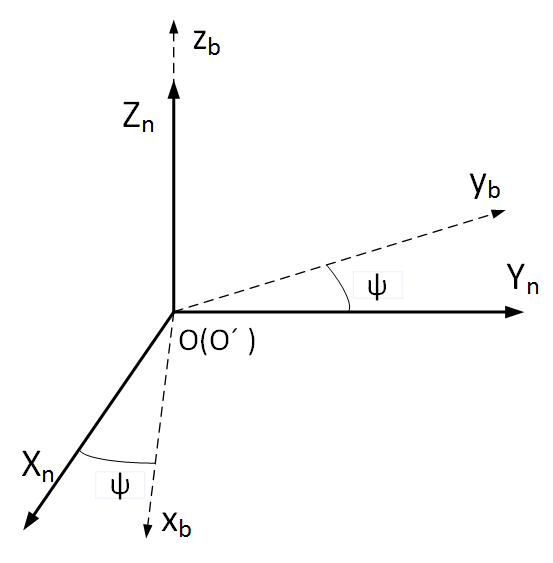
再经过R旋转回转到b系中,得到估计方向
\(\begin{bmatrix}
w.x \\
w.y \\
w.z
\end{bmatrix} =
\begin{bmatrix}
b.x \\
0 \\
b.z
\end{bmatrix}
\begin{bmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2)\\
2(q_1q_2+q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1)\\
2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & q_0^2-q_1^2-q_2^2+q_3^2\\
\end{bmatrix}\)
用估计方向与三轴方向进行叉乘求取方向误差
\(\begin{bmatrix} exMag \\eyMag \\ezMag \end{bmatrix}=
\begin{bmatrix} m.x \\m.y\\m.z\end{bmatrix} \times
\begin{bmatrix} w.x \\w.y\\w.z\end{bmatrix} =
\begin{bmatrix} m.y*w.z-m.z*w.y \\m.z*w.x-m.x*w.z \\m.x*w.y-m.y*w.x \end{bmatrix}\)
3、这部分只是用来修正YAW轴的,还要加上加速度的校正补偿项(上面的博文中已经推导过)。
\(\begin{bmatrix} ex \\ey \\ez \end{bmatrix}=
\begin{bmatrix} a.y*v.z-a.z*v.y \\a.z*v.x-a.x*v.z \\a.x*v.y-a.y*v.x \end{bmatrix} +
\begin{bmatrix} m.y*w.z-m.z*w.y \\m.z*w.x-m.x*w.z \\m.x*w.y-m.y*w.x \end{bmatrix}\)
4、对误差进行积分比例运算,更新陀螺仪角速度值,同理IMU。
void MahonyAHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz) {
float recipNorm;
float q0q0, q0q1, q0q2, q0q3, q1q1, q1q2, q1q3, q2q2, q2q3, q3q3;
float hx, hy, bx, bz;
float halfvx, halfvy, halfvz, halfwx, halfwy, halfwz;
float halfex, halfey, halfez;
float qa, qb, qc;
// Use IMU algorithm if magnetometer measurement invalid (avoids NaN in magnetometer normalisation)
if((mx == 0.0f) && (my == 0.0f) && (mz == 0.0f)) {
MahonyAHRSupdateIMU(gx, gy, gz, ax, ay, az);
return;
}
// Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)
if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) {
// Normalise accelerometer measurement
recipNorm = invSqrt(ax * ax + ay * ay + az * az);
ax *= recipNorm;
ay *= recipNorm;
az *= recipNorm;
// Normalise magnetometer measurement
recipNorm = invSqrt(mx * mx + my * my + mz * mz);
mx *= recipNorm;
my *= recipNorm;
mz *= recipNorm;
// Auxiliary variables to avoid repeated arithmetic
q0q0 = q0 * q0;
q0q1 = q0 * q1;
q0q2 = q0 * q2;
q0q3 = q0 * q3;
q1q1 = q1 * q1;
q1q2 = q1 * q2;
q1q3 = q1 * q3;
q2q2 = q2 * q2;
q2q3 = q2 * q3;
q3q3 = q3 * q3;
// Reference direction of Earth's magnetic field
hx = 2.0f * (mx * (0.5f - q2q2 - q3q3) + my * (q1q2 - q0q3) + mz * (q1q3 + q0q2));
hy = 2.0f * (mx * (q1q2 + q0q3) + my * (0.5f - q1q1 - q3q3) + mz * (q2q3 - q0q1));
bx = sqrt(hx * hx + hy * hy);
bz = 2.0f * (mx * (q1q3 - q0q2) + my * (q2q3 + q0q1) + mz * (0.5f - q1q1 - q2q2));
// Estimated direction of gravity and magnetic field
halfvx = q1q3 - q0q2;
halfvy = q0q1 + q2q3;
halfvz = q0q0 - 0.5f + q3q3;
halfwx = bx * (0.5f - q2q2 - q3q3) + bz * (q1q3 - q0q2);
halfwy = bx * (q1q2 - q0q3) + bz * (q0q1 + q2q3);
halfwz = bx * (q0q2 + q1q3) + bz * (0.5f - q1q1 - q2q2);
// Error is sum of cross product between estimated direction and measured direction of field vectors
halfex = (ay * halfvz - az * halfvy) + (my * halfwz - mz * halfwy);
halfey = (az * halfvx - ax * halfvz) + (mz * halfwx - mx * halfwz);
halfez = (ax * halfvy - ay * halfvx) + (mx * halfwy - my * halfwx);
// Compute and apply integral feedback if enabled
if(twoKi > 0.0f) {
integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki
integralFBy += twoKi * halfey * (1.0f / sampleFreq);
integralFBz += twoKi * halfez * (1.0f / sampleFreq);
gx += integralFBx; // apply integral feedback
gy += integralFBy;
gz += integralFBz;
}
else {
integralFBx = 0.0f; // prevent integral windup
integralFBy = 0.0f;
integralFBz = 0.0f;
}
// Apply proportional feedback
gx += twoKp * halfex;
gy += twoKp * halfey;
gz += twoKp * halfez;
}
// Integrate rate of change of quaternion
gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors
gy *= (0.5f * (1.0f / sampleFreq));
gz *= (0.5f * (1.0f / sampleFreq));
qa = q0;
qb = q1;
qc = q2;
q0 += (-qb * gx - qc * gy - q3 * gz);
q1 += (qa * gx + qc * gz - q3 * gy);
q2 += (qa * gy - qb * gz + q3 * gx);
q3 += (qa * gz + qb * gy - qc * gx);
// Normalise quaternion
recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= recipNorm;
q1 *= recipNorm;
q2 *= recipNorm;
q3 *= recipNorm;
}
